Comparison of Three Multi-armed Bandit Strategies

I- Introduction

In a previous article, I introduced the design and implementation of a multi-armed bandit (MAB) framework. This framework was built to simplify the implementation of new MAB strategies and provide a structured approach for their analysis.

Three strategies have already been integrated into the framework: RandomSelector, MaxAverageRewardSelector, and UpperConfidenceBoundSelector.

• The RandomSelector strategy selects arms at random, serving as a baseline for evaluating MAB strategies.
• The MaxAverageRewardSelector strategy pulls the arm with the highest observed average reward.
• The UpperConfidenceBoundSelector strategy (UCB) selects the arm with the highest upper bound of its expected reward confidence interval, balancing exploration and exploitation. This strategy is discussed in detail in this article.

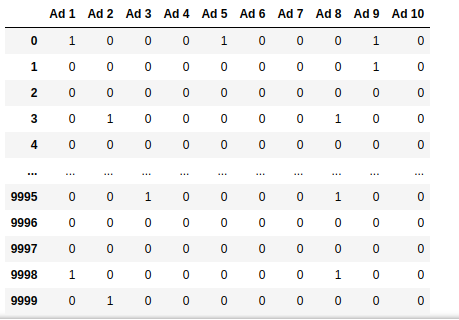
The dataset used in this study is detailed in this article. It consists of 10,000 observations, each representing a request to serve an ad through a pay-per-click advertising network. The dataset includes a total of 10 ads, each functioning as an arm of a multi-armed bandit (MAB).

Serving an ad to a user is equivalent to pulling an arm in the MAB framework. If the ad is clicked, the arm yields a reward of 1; if it is not clicked, the reward is 0.

I will analyze the baseline strategy, Max Average Reward, and UCB in sequence. For each strategy, we will evaluate its efficiency, identify the most frequently pulled arm, and examine how arm selections evolve over time. 

But first, let’s set up our three MAB instances.

import matplotlib.pyplot as plt
from matplotlib import colors
import pandas as pd
from multi_armed_bandit import *
from mab_plotting import MabPlotting
rnd_mab = MultiArmedBandit(RandomSelector(), dataset.values)
avg_mab = MultiArmedBandit(MaxAverageRewardSelector(), dataset.values)
ucb_mab = MultiArmedBandit(UpperConfidenceBoundSelector(), dataset.values)

The MAB framework is imported from the multi_armed_bandit module. Additionally, the MabPlotting class from the mab_plotting module provides utility functions for visualizing results. Its implementation is included in the appendix of this article.

II- The Baseline Strategy

Let's initiate the baseline MAB.

rnd_mab.play(num_rounds)

Now, let's retrieve the total reward collected by this strategy and evaluate its efficiency. 

total_reward_rnd = rnd_mab.get_total_reward()
efficiency_rnd = rnd_mab.get_efficiency()

print(f'Total reward of random MAB: {total_reward_rnd}, efficiency: {efficiency_rnd}.')

The total reward collected using a random arm selection strategy is 1,263. The efficiency of this baseline strategy is 0.166 (≈17%). Given that the maximum achievable reward in this dataset is 7,424, a purely random selection yields 1,263 dollars in revenue out of a potential 7,424 dollars, assuming each ad click generates 1 dollar in revenue. 

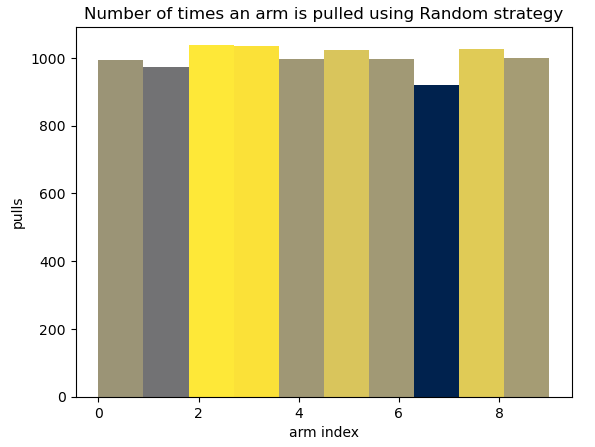
Next, let's examine the distribution of arm pulls for this strategy and determine how frequently each arm was selected.

MabPlotting.plot_num_pulls_histogram(plt, rnd_mab.get_pulled_arms(), 'Random')

The statement above generates the following histogram. As expected, the arms are pulled roughly the same number of times.

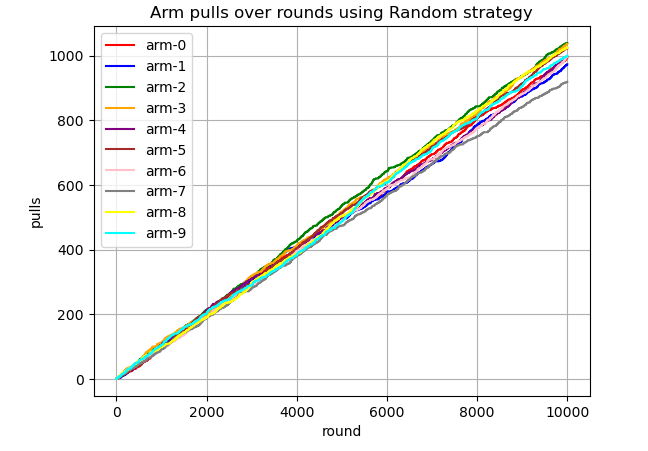
Now, let's check how each arm is being pulled over time (over rounds).

MabPlotting.plot_pulls_over_rounds(plt, rnd_mab.get_cumulative_pulls_by_round(), num_rounds, 'Random')

The figure below shows that the arms are pulled at approximately the same frequency over time.

III- The Maximum Average Reward Strategy

In this section, we perform the same analysis for the Maximum Average Reward (MAR) strategy as we did for the baseline strategy.

The MaximumAverageRewardSelector collects a total reward of 489, achieving an efficiency of 0.066 (≈7%). This is significantly lower than the 17% efficiency of the baseline strategy.

Let's see how frequently are arms pulled by MaximumAverageRewardSelector

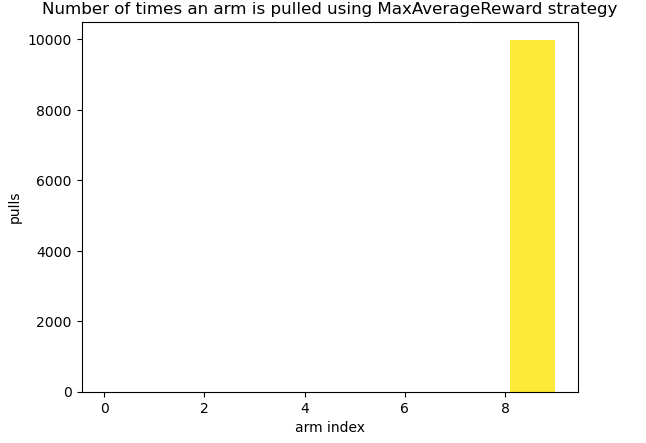
The Maximum Average Reward selection strategy pulls a single arm throughout the entire game—specifically, arm 9 (Ad10). This means the strategy locks onto one of the best-performing arms from the warm-up phase and continues pulling it for the remaining rounds without reassessing its choice. Clearly, this is a flawed approach.

One way to improve efficiency is to pull each arm randomly k times (where k > 1) before switching to the MaximumAverageRewardSelector. However, I will introduce a more effective improvement in a future article, where I discuss the exploration-exploitation trade-off in MAB strategies. For now, we will leave the MaximumAverageRewardSelector implementation unchanged.

Given its deterministic behavior, the arm pulls over time diagram is not particularly insightful and will be omitted.

IV- The Upper Confidence Bound Strategy

The UCB strategy achieves a total reward of 2,200, with an efficiency of 0.296 (≈30%), making it the most effective MAB strategy so far. The strategy identifies arm 4 (Ad5) as the best option and pulls it significantly more often than any other arm.

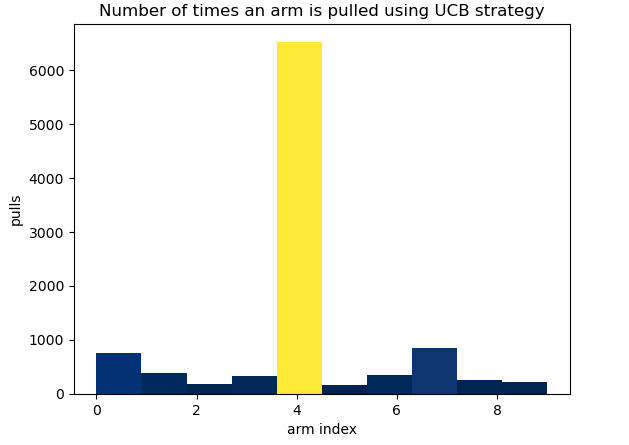
Unlike the Maximum Average Reward strategy, UCB does not exclusively settle on arm 4. Instead, it continues to explore other arms periodically throughout the MAB game, allowing itself the opportunity to discover potentially better-performing options. However, its efficiency remains relatively low, indicating room for improvement with more advanced MAB strategies.

Appendix

The implementation of the MabPlotting utility class is provided below.

from typing import List
from matplotlib import colors
import numpy as np

class MabPlotting:
    """
    Offers plotting functions to evaluate the performance of multi-armed bandit strategies.
    """
    @staticmethod
    def plot_num_pulls_histogram(plotter, pulled_arms: List[int], strategy: str) -> None:
        freqs, bins, patches = plotter.hist(pulled_arms)

        plotter.xlabel('arm index')
        plotter.ylabel('pulls')
        plotter.title(f'Number of times an arm is pulled using {strategy} strategy')
        
        norm_freqs = freqs / freqs.max() 
        norm = colors.Normalize(norm_freqs.min(), norm_freqs.max())

        for thisfrac, thispatch in zip(norm_freqs, patches):
            color = plotter.cm.cividis(norm(thisfrac))
            thispatch.set_facecolor(color)
        
        plotter.show()
   @staticmethod
    def plot_pulls_over_rounds(plotter, cum_pulls_by_round: List[List[int]], num_rounds: int, strategy: str) -> None:
        colors = ["red", "blue", "green", "orange", "purple", "brown", "pink", "gray", "yellow", "cyan"]
        cumul_pulls_np = np.array(cum_pulls_by_round)
        
        
        for i in range(0, 10):
            plotter.plot(range(0, num_rounds), cumul_pulls_np[:, i], color=colors[i], label=f'arm-{i}')
        
        plotter.xlabel('round')
        plotter.ylabel('pulls')
        plotter.title(f'Arm pulls over rounds using {strategy} strategy')
        plotter.grid()
        plotter.legend()
        plotter.show()
  @staticmethod
  def plot_reward_over_rounds(plotter, cumul_reward_by_round: List[int], num_rounds: int, strategy: str, color: str = 'blue') -> None:
        plotter.plot(range(0, num_rounds), cumul_reward_by_round, color=color)
        plotter.xlabel('round')
        plotter.ylabel('reward')
        plotter.title(f'Collected reward over rounds using {strategy} strategy')
        plotter.grid()
        plotter.show()