In previous blog posts, we explored the multi-armed bandit (MAB) problem and discussed the Upper Confidence Bound (UCB) algorithm as one approach to solving it. Research literature has introduced multiple algorithms for tackling this problem, and there is always room for experimenting with new ideas. To facilitate the implementation and comparison of different algorithms, we introduce a framework for MAB solvers. Here, we start with a simple design, which we will extend and refine in future articles.
I- The Design
The proposed framework design is presented below.
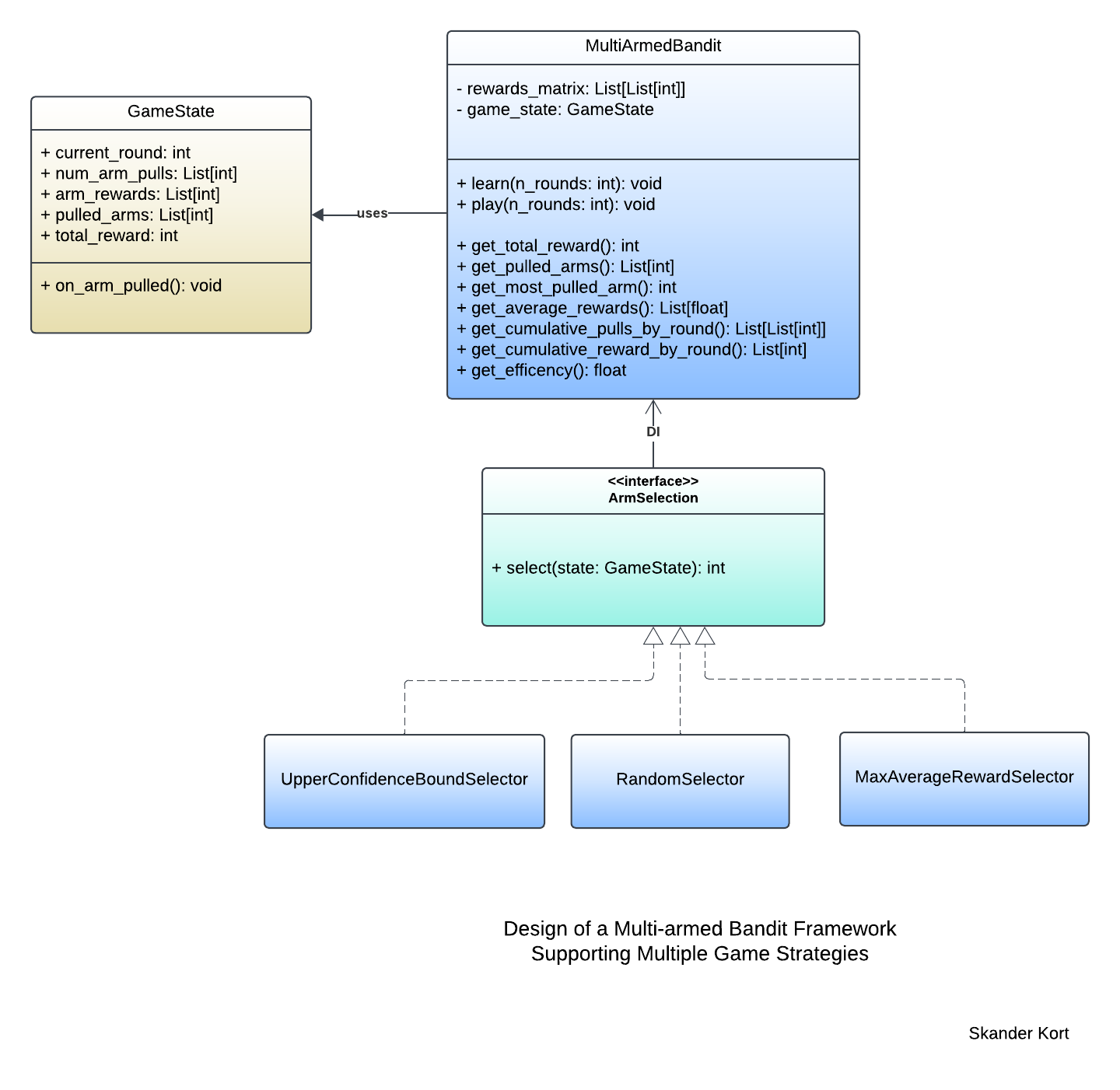
The core class in this design is MultiArmedBandit, which represents instances of a multi-armed bandit (MAB) game. The rewards_matrix attribute stores game data, where each row corresponds to a round and each column represents an arm. The game_state attribute, an instance of the GameState class, maintains the current state of the game.
The game is initiated through the play() method, while additional methods facilitate the collection of key performance metrics. Since MAB problems are also a subset of reinforcement learning, the MultiArmedBandit API includes a learn() method, which serves as an alias for play() (or vice versa), reinforcing the idea that playing the game inherently involves learning from rewards.
MAB strategies are implementations of the ArmSelection interface and are injected into MultiArmedBandit instances. These strategies must implement the select() method, which determines the next arm to pull based on the current state of the game. Examples of such strategies include UpperConfidenceBoundSelector, RandomSelector, and MaxAverageRewardSelector.
The states of MAB games are represented by instances of the GameState class. Each state consists of private attributes that track various aspects of the game:
current_round: Indicates the current round of the game.num_arm_selections: Stores the number of times each arm has been pulled up to the current round.arm_rewards: Tracks the cumulative reward accumulated by each arm throughout the game.selected_arms: Records the arm selected at each round by the MAB strategy.total_reward: This attribute tracks the total reward accumulated during play. While it does not influence decision-making, it serves as a key metric for comparing different arm selection strategies.
This design follows the separation of concerns principle. The MultiArmedBandit class is responsible for managing the game, executing it round by round. At each round, arm selection is delegated to an ArmSelection strategy, ensuring modular decision-making. Once an arm is selected, the GameState class is notified to update accordingly. Further refinements to this design will be explored in future posts.
Now, let's turn our attention to implementing the design outlined above.
II- The Implementation
Before diving into the implementation of each class, let's first list the necessary imports for this MAB framework.
import math
import random
import copy
from abc import ABC, abstractmethod
from typing import List, Optional1. Keeping Track of Game States
The GameState class is responsible for tracking the multi-armed bandit game. Its implementation is provided below.
class GameState:
"""
Data class to hold the state of a multi-armed bandit game. Clones of GameState should be
passed to arm-selection strategies to prevent said-strategies from tampering with the state
of the multi-armed bandit game.
"""
def __init__(self, num_arms: int):
self.num_arms = num_arms
self.current_round: int = 0
self.num_arms_pulls: List[int] = [0] * num_arms
self.arms_rewards: List[int] = [0] * num_arms
self.pulled_arms: List[int] = []
self.total_reward = 0
def on_arm_pulled(self, arm_idx: int, arm_reward: int) -> None:
"""
Updates game state on an arm pulled event.
"""
self.num_arms_pulls[arm_idx] += 1
self.arms_rewards[arm_idx] += arm_reward
self.total_reward += arm_reward # Not used for decision make, but a convinient way to update this game metric.
self.pulled_arms.append(arm_idx)
self.current_round += 1
Encapsulating the state of the multi-armed bandit (MAB) in a separate class enables MultiArmedBandit to efficiently pass the game state to ArmSelection strategies. Additionally, this separation keeps MultiArmedBandit free from the complexity of managing state updates. Ideally, ArmSelection strategies should not be able to modify this state. However, since Python lacks built-in access modifiers, an alternative approach is required to enforce this restriction. More on this later.
on_arm_pulled() functions as an event handler, triggered whenever an arm is pulled to update the state of the multi-armed bandit (MAB) game. It increments the pull count for the selected arm and updates the total reward accumulated by that arm. Additionally, it records the arms pulled in each round, tracks the overall reward collected so far, and maintains the current round index.
2. Arm Selection Strategies
To implement ArmSelection, we use Python's Abstract Base Class (ABC) as a substitute for built-in interfaces and traits.
class ArmSelection(ABC):
"""
Strategy for selecting an arm.
"""
@abstractmethod
def select(self, game_state: GameState) -> int:
pass
At this stage, we are ready to implement the three concrete arm selection strategies outlined in the design diagram above. The upper confidence bound strategy has already been covered in a previous post.
class UpperConfidenceBoundSelector(ArmSelection):
def select(self, game_state: GameState) -> int:
best_arm: Optional[int] = None
max_ucb = 0.0
for candidate_arm in range(game_state.num_arms):
average_reward = float(game_state.arms_rewards[candidate_arm]) / game_state.num_arms_pulls[candidate_arm]
delta = math.sqrt(1.5 * math.log(game_state.current_round + 1) / game_state.num_arms_pulls[candidate_arm]) # Regularization term
ucb = average_reward + delta
if ucb >= max_ucb:
max_ucb = ucb
best_arm = candidate_arm
return best_arm
The maximum average reward strategy closely resembles the UCB strategy, except that it lacks a regularization term in the formula used to calculate an arm's score.
class MaxAverageRewardSelector(ArmSelection):
def select(self, game_state: GameState) -> int:
best_arm: Optional[int] = None
max_avg_reward = 0.0
for candidate_arm in range(game_state.num_arms):
avg_reward = float(game_state.arms_rewards[candidate_arm]) / game_state.num_arms_pulls[candidate_arm]
if avg_reward >= max_avg_reward:
max_avg_reward = avg_reward
best_arm = candidate_arm
return best_armThe implementation of the random selection strategy is self-explanatory.
class RandomSelector(ArmSelection):
def select(self, game_state: GameState) -> int:
return random.randrange(game_state.num_arms)3. The Multi-armed Bandit Class
Finally, let's dive into the implementation of the core class in this framework: MultiArmedBandit.
3.1 Class constructor
The implementation of MultiArmedBandit 's constructor is shown below.
class MultiArmedBandit:
def __init__(self, arm_selector: ArmSelection, rewards_matrix: List[List[int]]):
"""
Top-level class.
Args:
arm_selector: Arm selection strategy.
rewards_matrix: rewards_matrix[i][j] is the reward yielded by arm <j> at round <i>.
"""
MultiArmedBandit.__validate_rewards_matrix(rewards_matrix)
# Set a seed to ensure reproducibility.
random.seed(2025)
self.__arm_selector = arm_selector
self.__rewards_matrix = rewards_matrix
self.__max_rounds = len(rewards_matrix)
self.__num_arms = len(rewards_matrix[0])
self.__game_state = GameState(self.__num_arms)
@staticmethod
def __validate_rewards_matrix(rewards_matrix: List[List[int]]) -> None:
if len(rewards_matrix) == 0:
raise ValueError('Rewards matrix is empty!')
l = len(rewards_matrix[0])
if l == 0:
raise ValueError('First row of rewards matrix is empty!')
if any(len(row) != l for row in rewards_matrix):
raise ValueError('Rewards matrix rows must have the same length!')
if len(rewards_matrix) < l:
raise ValueError('Number of rounds should be greater or equal to the number of arms to allow warming up the arms!')
The class constructor takes an arm selection strategy and multi-armed bandit data as input. Before proceeding, the MAB data is validated using the static method __validate_rewards_matrix, ensuring that the rewards matrix is non-empty and that all rows have the same length. Once validated, the constructor initializes private attributes and creates a new game state.
3.2 Learning to play
The play logic is shown below.
def play(self, num_rounds: int) -> None:
self.learn(num_rounds)
def learn(self, num_rounds: int) -> None:
self.__validate_rounds_to_play(num_rounds)
self.__game_state = GameState(self.__num_arms)
self.__warm_up_arms()
self.__select_pull_arms()
def __validate_rounds_to_play(self, num_rounds: int) -> None:
if num_rounds < self.__num_arms:
raise ValueError(f'Number of rounds must be greater than ${self.__num_arm}!')
if num_rounds > self.__max_rounds:
raise ValueError(f'Number of rounds cannot exceed ${self.__max_rounds}!')
def __warm_up_arms(self) -> None:
"""
Pulls each arm once in a random order. Strategies like UCB require every arm to be pulled at least once.
This initial exploration (warm-up) should not negatively impact strategies that do not require it.
"""
shuffled_arms = list(range(self.__num_arms))
random.shuffle(shuffled_arms)
for round_idx in range(self.__num_arms):
self.__pull_single_arm(shuffled_arms[round_idx])
def __pull_single_arm(self, arm_idx: int) -> None:
current_round = self.__game_state.current_round
self.__game_state.on_arm_pulled(arm_idx, self.__rewards_matrix[current_round][arm_idx])
def __select_pull_arms(self) -> None:
"""
Selects an arm per ArmSelection strategy, then pulls it.
"""
for _ in range(self.__game_state.current_round, self.__max_rounds):
rnd = random.random()
if rnd <= self.__eps_greedy_rate:
selected_arms_idx = random.randrange(self.__num_arms)
else:
selected_arms_idx = self.__arm_selector.select(copy.deepcopy(self.__game_state))
self.__pull_single_arm(selected_arms_idx)
The multi-armed bandit can be initiated by calling either the play() or learn() method, with play() serving as an alias for learn(). When a new game starts, learn() first validates the number of rounds, warms up the bandit arms by pulling each arm once (using the __warm_up_arms() method), and then begins the actual gameplay by calling __select_pull_arms(). It is important to note that many arm selection strategies assume that each arm has been pulled at least once before making informed selections.
The __select_pull_arms() method is straightforward, as arm selection is delegated to the injected arm selection strategy. During each round, an arm is selected and subsequently pulled via the __pull_single_arm() method. Pulling an arm triggers the GameState to update itself by invoking the event handler on_arm_pulled().
Additionally, __select_pull_arms() deep-copies the game state before passing it to the arm selection strategy. This precaution prevents unintended state mutations by the strategy. However, this approach introduces some computational overhead. The framework's performance testing will determine whether this overhead is acceptable.
3.3 Game metrics
The implementations of get_total_reward(), get_pulled_arms(), get_most_pulled_arm(), and get_average_rewards() are straightforward and intuitive, requiring no additional explanation.
def get_total_reward(self) -> int:
return self.__game_state.total_reward
def get_pulled_arms(self) -> List[int]:
return self.__game_state.pulled_arms
def get_most_pulled_arm(self) -> int:
arm_pulls = self.__game_state.arm_pulls
max_pulls = max(arm_pulls)
def get_average_rewards(self) -> List[float]:
state = self.__game_state
return [float(state.arms_rewards[arm]) / state.num_arms_pulls[arm] for arm in range(0, self.__num_arms)] The get_efficiency() method is crucial for comparing different arm selection strategies. It computes the ratio of the total reward obtained by a strategy to the maximum possible reward in the game (the optimal reward). This metric helps assess how well a strategy performs relative to the best achievable outcome. Its implementation is shown below.
def get_efficiency(self) -> Optional[float]:
"""
Calculates game efficiency as received reward divided by optimum reward.
"""
max_reward = sum(max(row) for row in self.__rewards_matrix)
if max_reward > 0:
return float(self.__game_state.total_reward) / max_reward
else:
return NoneFinally, we present the implementation of two methods designed to analyze the behavior of MAB strategies over time: get_cumulative_pulls_by_round() and get_cumulative_reward_by_round().
The get_cumulative_pulls_by_round() method calculates, for each arm and each round, the total number of times the arm has been pulled up to that round. This provides insight into how frequently each arm is selected throughout the game. Its implementation is shown below.
def get_cumulative_pulls_by_round(self) -> List[List[int]]:
"""
Calculates the number of pulls of each arm up to some round, for all rounds.
"""
state = self.__game_state
cumul_pulls = [[0] * self.__num_arms]
for pulled_arm in state.pulled_arms:
last_pulls = cumul_pulls[-1].copy()
last_pulls[pulled_arm] += 1
cumul_pulls.append(last_pulls)
cumul_pulls.pop(0)
return cumul_pullsSimilarly, the get_cumulative_reward_by_round() method calculates the total reward accumulated by the MAB strategy up to each round. This provides insight into how quickly the strategy identifies the best arm and begins consistently collecting rewards over time.
def get_cumulative_reward_by_round(self) -> List[int]:
"""
Returns the total reward over rounds.
"""
state = self.__game_state
cumul_reward = []
total_reward = 0
for round_idx in range(state.current_round):
pulled_arm = state.pulled_arms[round_idx]
total_reward += self.__rewards_matrix[round_idx][pulled_arm]
cumul_reward.append(total_reward)
return cumul_rewardIII. Concluding Remarks
In this article, I presented a design for an MAB framework and demonstrated its implementation in Python. The design adheres to the Single Responsibility Principle, with the arm selection logic separated from the MultiArmedBandit class. This modular approach facilitates the comparison of different MAB strategies, which will be explored in a future article.