Thompson Sampling With Gaussian Distribution - A Stochastic Multi-armed Bandit

By Skander, 8 December, 2024

A Thompson Sampling algorithm using a Beta probability distribution was introduced in a previous post. The Beta distribution is well-suited for binary multi-armed bandits (MABs), where arm rewards are restricted to values of 0 or 1.

In this article, we introduce an alternative MAB sampling algorithm designed for the more general case where arm rewards are continuous: Thompson Sampling with a Gaussian Distribution (TSG).

I- Thompson Sampling With Gaussian Distribution

Like Thompson Sampling with a Beta distribution (TSB), the Thompson Sampling with a Gaussian distribution (TSG) algorithm treats each MAB arm as a random variable, samples a value from an appropriate probability distribution, updates its prior belief, and selects the arm that maximizes the sampled value. However, the interpretation of the sampled value differs between TSB and TSG.

In TSB, the sampled value from the Beta distribution represents the probability of success, meaning the likelihood that an arm yields a reward of 1.
In TSG, the sampled value from the Gaussian distribution is interpreted as an estimate of the arm’s average reward, rather than a probability of success.

More specifically, consider the Gaussian distribution function: $$g(x | \mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} exp(-\frac{(x - \mu)^2}{2 \sigma^2}))$$ where,

$x$: a random variable in $]-\infty , +\infty[$.
$\mu$: mean value of $x$.
$\sigma$: standard deviation of $x$.

TSG begins with a prior mean reward $\mu$ and a prior standard deviation $\sigma$ for each arm. The initial mean $\mu$ can be estimated by randomly pulling each arm and computing the observed average reward, a process known as warming up the arms. For the standard deviation $\sigma$, it is common practice to start with a fixed value (e.g., 1) for all arms.

After each round of the MAB process:

The prior mean of the selected arm is updated based on the newly observed average reward.
The prior standard deviation is gradually reduced, typically by dividing it by either the number of times an arm has been pulled or its square root.

As more rounds are played, the Gaussian distributions of the arms become narrower, reflecting reduced uncertainty in reward estimates. This shrinking variance ensures that the algorithm progressively shifts from exploration to exploitation, as confidence in the estimated rewards increases.

II- Implementation

Thompson Sampling with a Gaussian Distribution (TSG) seamlessly integrates into the MAB framework as an implementation of the ArmSelection interface, encapsulated in the ThompsonGaussianSampling class. Unlike the MAB strategies implemented so far, ThompsonGaussianSampling introduces a new parameter in its constructor: sigma, which represents the initial prior standard deviation of arm rewards.

As usual, the core selection logic is implemented in the select() method, which follows these steps:

Iterate through all MAB arms.
Estimate the prior mean reward for each arm by dividing the total collected reward by the number of times the arm has been pulled.
Refine the prior standard deviation by adjusting it based on the number of times the arm has been played—typically by dividing its current value by the square root of the pull count.
Sample a value from a Gaussian distribution parameterized by the updated priors.
Select the arm that maximizes the expected average reward, ensuring a balance between exploration and exploitation.

class ThompsonGaussianSampling(ArmSelection):
    """
    Thompson Sampling for multi-armed bandits with continuous rewards assumes that each arm follows a Gaussian distribution. 
    """
    def __init__(self, sigma: float = 1):
        """
        Args:
            sigma (float): Standard deviation of the reward random variable. Assumes all arms share the same sigma.
                   This parameter influences the algorithm's balance between exploration and exploitation.
        """
        if sigma <= 0:
            raise ValueError('Argument sigma must be positive!')
        
        self.__sigma = sigma
    def select(self, game_state: GameState) -> int:
        best_arm: Optional[int] = None
        max_sampled_avg = float('-inf')
        for candidate_arm in range(game_state.num_arms):
            num_pulls = game_state.num_arms_pulls[candidate_arm]
            prior_mu = float(game_state.arms_rewards[candidate_arm]) / num_pulls
            prior_sigma = self.__sigma / math.sqrt(num_pulls) # Less explorative as an arm is pulled.
            sampled_avg_reward = random.normalvariate(prior_mu, prior_sigma)
            if (sampled_avg_reward >= max_sampled_avg):
                max_sampled_avg = sampled_avg_reward
                best_arm = candidate_arm 
        return best_armclass ThompsonGaussianSampling(ArmSelection):
    """
    Thompson Sampling for multi-armed bandits with continuous rewards assumes that each arm follows a Gaussian distribution. 
    """
    def __init__(self, sigma: float = 1):
        """
        Args:
            sigma (float): Standard deviation of the reward random variable. Assumes all arms share the same sigma.
                   This parameter influences the algorithm's balance between exploration and exploitation.
        """
        if sigma <= 0:
            raise ValueError('Argument sigma must be positive!')
        
        self.__sigma = sigma
    def select(self, game_state: GameState) -> int:
        best_arm: Optional[int] = None
        max_sampled_avg = float('-inf')
        for candidate_arm in range(game_state.num_arms):
            num_pulls = game_state.num_arms_pulls[candidate_arm]
            prior_mu = float(game_state.arms_rewards[candidate_arm]) / num_pulls
            prior_sigma = self.__sigma / math.sqrt(num_pulls) # Less explorative as an arm is pulled.
            sampled_avg_reward = random.normalvariate(prior_mu, prior_sigma)
            if (sampled_avg_reward >= max_sampled_avg):
                max_sampled_avg = sampled_avg_reward
                best_arm = candidate_arm 
        return best_arm

III- Evaluation

Now, let's evaluate the performance of Thompson Sampling with a Gaussian Distribution and compare it to existing MAB algorithms. To ensure consistency, we will use the same dataset presented in the UCB analysis article.

Although the rewards in this dataset are binary, we can still leverage the Gaussian distribution to estimate the expected rewards. Additionally, since TSG is a parameterized strategy that accepts an initial prior standard deviation (sigma_prior) as input, we will assess its performance across different values of this parameter.

To facilitate this analysis, we define the following function:

def grid_search_sigma(sigma_range: np.ndarray, rounds: int) -> List[float]:
    return [MultiArmedBandit(ThompsonGaussianSampling(sigma), dataset.values).play(rounds).get_efficiency() for sigma in sigma_range]

Note that the MultiArmedBandit API has been slightly modified to support method chaining, enabling the streamlined call structure shown above.

Evaluating the efficiency of TSG for sigma_prior values ranging from 0.1 to 2, with a step size of 0.01, and visualizing the results produces the figure below.

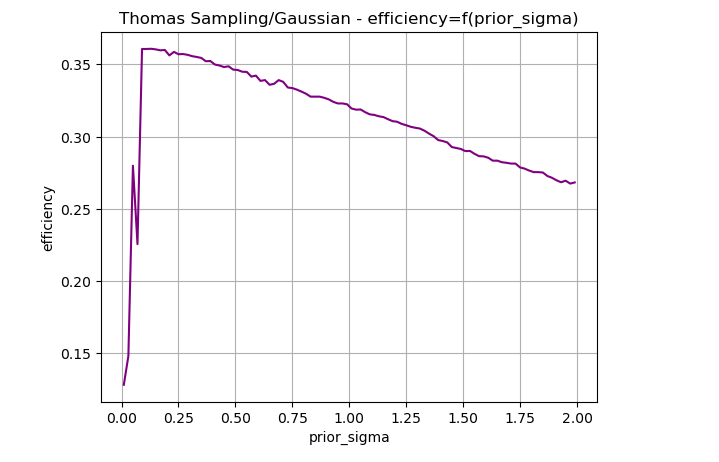
Efficience as a function of prior sigma in thompson sampling with Gausssian

We observe that efficiency increases as a function of prior_sigma, peaking at 36%, before steadily declining. The highest efficiency is achieved when sigma_prior = 0.1, making it the best-performing strategy on the given dataset.

For comparison:

Baseline algorithm: 16% efficiency
Thompson Sampling with a Beta Distribution (TSB): 35% efficiency (second-best)
Epsilon-greedy Maximum Average Reward (MAR): 34% efficiency
Upper Confidence Bound (UCB): 30% efficiency
Deterministic Maximum Average Reward (MAR): lowest performance (7%), as it is purely exploitative and lacks exploration

This slight improvement in performance compared to TSB can be attributed to the fact that TSG is even more aggressive in selecting Arm-4, which it identifies as optimal after several rounds. As shown in the figure below.

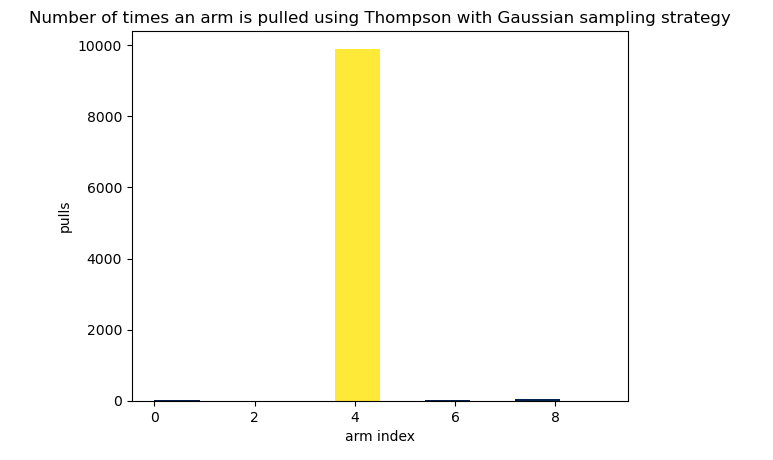
Thompson Gaussian MAB distribution of pulls

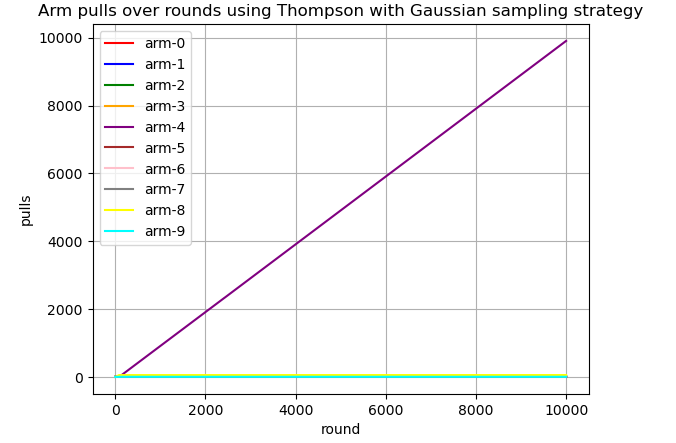
Visualizing the arm selection pattern of TSG over multiple rounds confirms the algorithm's convergence toward Arm-4, as illustrated in the figure below.

Thomson sampling Gaussian - pulls over time

IV- Concluding Remarks

We have explored a general, parameterized, and stochastic strategy for the multi-armed bandit (MAB) problem. This approach achieves the highest efficiency on an online marketing dataset. However, its superior performance may stem from overly aggressive exploitation of the arm identified as optimal after several rounds.

Further research is needed to refine this strategy. One key limitation is that early high-reward arms may deteriorate over time. If the algorithm prematurely locks onto the first identified "best" arm, it may fail to adapt to changing conditions. The exploration techniques covered so far have not enabled MAB algorithms to identify new optimal arms dynamically.

A promising direction for improvement could be developing adaptive forgetting mechanisms, allowing the algorithm to "unlearn" past decisions and re-evaluate arm rankings over time. Such an approach could make MAB strategies more flexible, enabling them to explore alternative candidates more effectively and adapt to non-stationary environments.

Add new comment